3x3
Games can (arguably) be characterized as satisfying two goals; being easy-to-play and having large-user-control over the result. Games that are easy-to-play include fruit-machines, bingo, roulette, pachinko, snakes-and-ladders, rock-paper-scissors, snap and most patience card-games. Ones that have large-user-control include chess, bridge, poker, scrabble, vintage-pinball (without flippers) and most multi-player card-games. The few that satisfy both goals are (arguably) checkers/drafts, dominoes, monopoly, modern-pinball (with flippers) and many video-games from pong onwards. 3x3 (three-by-three) is a patience card-game designed to join these few by being both easy-to-play and having a large-user-control over the result.
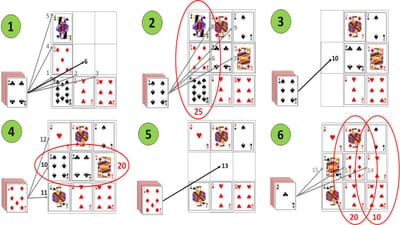
3x3 is so simple-to-play it actually easier to explain in a single paragraph of words rather than pictures. Take a pack-of-cards, and if it has no jokers, remove/discard a single court-card (jack, queen or king), then shuffle it. Then turn-over the top card, and place it in an empty "square" anywhere you like in a 3x3 grid (hence the name!), and continue until the grid is full. If at any time the sum of cards in a row, column or diagonal add-up to a number that is divisible by five, they can be removed from the grid (court-cards and jokers count as 10). You win if all the cards from the deck and grid are removed, otherwise you lose. The accompanying diagrams show an example game of 3x3 utilizing some common tactics and strategies.
In-diagram-1 the grid is being filled from the left-to-right, bottom-to-top. The queen is placed out-of-sequence in the top-left "square" as this ensures the sum-of-cards in the first-column is divisible by five (10 + 5 + 10 = 25 = 5 x 5). In-diagram-2 the rest of the grid is populated left-to-right, bottom-to-top. In-diagram-3 the cards in the first-column are then removed/discarded.
In-diagram-4 the first-column is then re-populated, with the six immediately placed in the centre as this ensures the sum-of-cards in the middle-row is divisible by five (6 + 4 + 10 = 20 = 5 x 4). In-diagram-5 the cards in the middle-row are then removed/discarded.
In-diagram-6 the middle-row is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (3 + 7 + 10 = 20 = 5 x 4). The two is then placed to the right as this ensures the sum-of-cards in the right-row is also divisible by five (4 + 2 + 2 = 10 = 5 x 2), before the king is placed to the left.
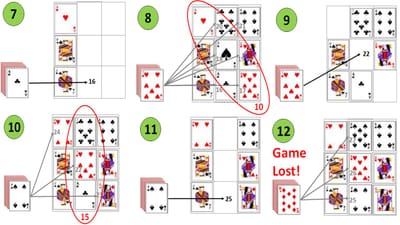
In-diagram-7 the cards in the middle-and-right-rows are then removed/discarded. In-diagram-8 the middle-and-right-rows are then re-populated, left-to-right, bottom-to-top, and somewhat-luckily, the sum-of-cards in the backslash-diagonal is divisible by five (1 + 1 + 8 = 10 = 5 x 2). In-diagram-9 the cards in the backslash-diagonal are then removed/discarded.
In-diagram-10 the backslash-diagonal is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (1 + 7 + 7 = 15 = 5 x 3). In-diagram-11 the cards in the middle-column are then removed/discarded. In-diagram-12 the middle-column is then re-populated, bottom-top. Unfortunately this results in no rows, columns or diagonals being divisible by 5, and the game is lost.
The above example highlights some tactics and strategies that can increase the chances of winning the game, including planning to remove horizontal and vertical rows alternatively, and being aware that cards that count as ten are much more common than others. Also, placing a card that is divisible by five in the central "square" creates four opportunities for cards that count as five or ten to complete a removable threesome (1 row, 1 column and 2 diagonals), whereas placing it in a corner creates three opportunities (1 row, 1 column and 1 diagonal), leaving just two opportunities anywhere else (1 row and 1 column). An additional strategy is card counting; cards that are removed/discarded will weight the likelihood of subsequent ones having a different value.
The game can be made easier-or-harder by subtlety changing the rules. The easiest game includes the divisor being five, diagonals being removable, and the grid can migrate (i.e. if there are just two rows populated, the re-populated row can be placed above or below them, and likewise for columns). With these lax rules in-place, and with significant-player-experience, leads towards fifty-percent of games being winnable.
The hardest game includes the divisor being ten, diagonals not-being removable, and the grid cannot migrate (i.e. if there are just two rows populated, re-population can only occur in the empty-row, and likewise for columns). With these stringent rules in-place, winning is a significant challenge!
Finally, what the best tactics and strategies are, and the resulting likelihood of winning the game, is a non-trivial mathematical calculation that the author has not even attempted to ascertain!
3x3 is so simple-to-play it actually easier to explain in a single paragraph of words rather than pictures. Take a pack-of-cards, and if it has no jokers, remove/discard a single court-card (jack, queen or king), then shuffle it. Then turn-over the top card, and place it in an empty "square" anywhere you like in a 3x3 grid (hence the name!), and continue until the grid is full. If at any time the sum of cards in a row, column or diagonal add-up to a number that is divisible by five, they can be removed from the grid (court-cards and jokers count as 10). You win if all the cards from the deck and grid are removed, otherwise you lose. The accompanying diagrams show an example game of 3x3 utilizing some common tactics and strategies.
In-diagram-1 the grid is being filled from the left-to-right, bottom-to-top. The queen is placed out-of-sequence in the top-left "square" as this ensures the sum-of-cards in the first-column is divisible by five (10 + 5 + 10 = 25 = 5 x 5). In-diagram-2 the rest of the grid is populated left-to-right, bottom-to-top. In-diagram-3 the cards in the first-column are then removed/discarded.
In-diagram-4 the first-column is then re-populated, with the six immediately placed in the centre as this ensures the sum-of-cards in the middle-row is divisible by five (6 + 4 + 10 = 20 = 5 x 4). In-diagram-5 the cards in the middle-row are then removed/discarded.
In-diagram-6 the middle-row is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (3 + 7 + 10 = 20 = 5 x 4). The two is then placed to the right as this ensures the sum-of-cards in the right-row is also divisible by five (4 + 2 + 2 = 10 = 5 x 2), before the king is placed to the left.
In-diagram-7 the cards in the middle-and-right-rows are then removed/discarded. In-diagram-8 the middle-and-right-rows are then re-populated, left-to-right, bottom-to-top, and somewhat-luckily, the sum-of-cards in the backslash-diagonal is divisible by five (1 + 1 + 8 = 10 = 5 x 2). In-diagram-9 the cards in the backslash-diagonal are then removed/discarded.
In-diagram-10 the backslash-diagonal is then re-populated, with the seven immediately placed at the centre as this ensures the sum-of-cards in the middle-column is divisible by five (1 + 7 + 7 = 15 = 5 x 3). In-diagram-11 the cards in the middle-column are then removed/discarded. In-diagram-12 the middle-column is then re-populated, bottom-top. Unfortunately this results in no rows, columns or diagonals being divisible by 5, and the game is lost.
The above example highlights some tactics and strategies that can increase the chances of winning the game, including planning to remove horizontal and vertical rows alternatively, and being aware that cards that count as ten are much more common than others. Also, placing a card that is divisible by five in the central "square" creates four opportunities for cards that count as five or ten to complete a removable threesome (1 row, 1 column and 2 diagonals), whereas placing it in a corner creates three opportunities (1 row, 1 column and 1 diagonal), leaving just two opportunities anywhere else (1 row and 1 column). An additional strategy is card counting; cards that are removed/discarded will weight the likelihood of subsequent ones having a different value.
The game can be made easier-or-harder by subtlety changing the rules. The easiest game includes the divisor being five, diagonals being removable, and the grid can migrate (i.e. if there are just two rows populated, the re-populated row can be placed above or below them, and likewise for columns). With these lax rules in-place, and with significant-player-experience, leads towards fifty-percent of games being winnable.
The hardest game includes the divisor being ten, diagonals not-being removable, and the grid cannot migrate (i.e. if there are just two rows populated, re-population can only occur in the empty-row, and likewise for columns). With these stringent rules in-place, winning is a significant challenge!
Finally, what the best tactics and strategies are, and the resulting likelihood of winning the game, is a non-trivial mathematical calculation that the author has not even attempted to ascertain!
