Striped-Trie
A striped-trie (an "STrie" for short - the Downloads web-page contains examples and white-papers) is a data-structure optimized for input-output performance for near key/entry matches (i.e. for next and previous key/entry location and maintenance - not just exact matches as in other algorithms such as hashing).
Goal: A trie data-structure optimized for use in the spectral data-model & other applications (e.g. data sorting, retrieval & maintenance etc.)
Problem: Standard tries are inefficient at data-storage and sub-optimal in near key/entry matching
Solution: Minimize data-storage and maximize near key/entry location performance
Mechanism: A 256 bit ascii pointer vector approach in combination with meta-data striping/clustering
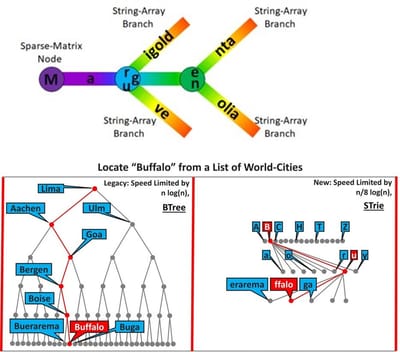
The first accompanying trie diagram of 4 colours has 3 nodes and 6 branches (one of which is empty). Navigating from the root-node outwards through all the branches and sub-nodes returns the 4 colours "Marigold, Magenta, Magnolia and Mauve" (the 4 keys/entries) as a sorted sequence.
In general, if n is the number of keys/entries and n+ the number of nodes, the nodes are represented as a 256 bit ascii pointer vector ("IT-speak"!). In perhaps simpler-but-equivalent "math-speak", they are represented as a sparse 2-dimensional integer matrix of n+ rows (the nodes) and 256 columns (the ascii character-set). This forms a "DNA" sequence of characters/symbols that navigates from the root-node outwards and reconstructs each individual key/entry.
The second accompanying diagram demonstrates STrie's superiority over BTree in that having multiple branches per node results in less processing levels being required to locate a key/entry. The maximum of 256 branches for each node results in 8 times fewer levels (2 ^ 8 = 256), giving a rough-and-ready speed-limiter of n(log (n) / 8 in "big O" notation; 8 times faster.
Branches are represented as a 1-dimensional string-array of n+ rows. This forms a "junk-DNA" sequence of characters/symbols which do not affect the "node-navigation", but do contribute to the reconstruction of the key/entry. This "junk-DNA" usually comes at and/or near the end of keys (e.g. "ffalo" in "Buffalo"), but can occur anywhere (e.g. "est " in "West Carson" and "West Chester"). If a row-pointer is non-zero its column-position represents the ascii code concerned (e.g. a 123 in column 102 means "B"s are located in row 123, and a 4567 in column 165 means "u"s are located in row 4567).
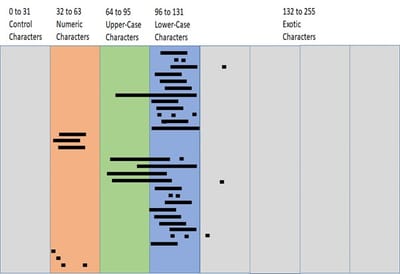
The third accompanying striping/clustering diagram shows how the sparse integer matrix is refined by meta-data which indicates where non-zero row-pointers occur within the nodes (i.e. "where the action is"). The vertical stripes partition the ascii character-set into like-bands where data tends to cluster (e.g. alphabetics, numbers, etc.). The horizontal lines and points demarcate within each node where the data actually clusters which minimizes the number of linear-scans required. In this implementation if there are 3 or less row-pointers they are represented as point-vectors (e.g. "r", "g" and "u"), otherwise they are represented as a range-vector and a single point-vector (e.g. "B to Q" and "Z").
This approach is essential to maximize near key/entry location performance which is required to out-compete current algorithms that sort, retrieve and maintain data (e.g. QuickSort, BinarySearch and BTree etc.). These are required for applications such as symbolic-processors, sort-engines, spell-checkers and text-auto-fillers, dictionaries, relational and NoSQL databases, file-systems, etc.
The Downloads web-page contains working-examples and white-papers of STrie versus QuickSort (50+ percent faster), STrie versus BinarySearch (350% faster) and STrie versus BTree (100+ percent faster). The proof-of-concept code is written in MS VBA which was chosen for its ability to seamlessly integrate with Excel.
Although these are significant the compelling differentiator of the algorithm is its suitability for massive parallelization. Both data and processing can easily be spread across CPUs. The simplest way of doing this would be to front-end the algorithm with a triaging routine that distributes data (and hence processing) to 1 of 256 CPUs, based on the initial character of the STrie. A more sophisticated triaging routine would better-balance loads based on usage criteria.
Goal: A trie data-structure optimized for use in the spectral data-model & other applications (e.g. data sorting, retrieval & maintenance etc.)
Problem: Standard tries are inefficient at data-storage and sub-optimal in near key/entry matching
Solution: Minimize data-storage and maximize near key/entry location performance
Mechanism: A 256 bit ascii pointer vector approach in combination with meta-data striping/clustering
The first accompanying trie diagram of 4 colours has 3 nodes and 6 branches (one of which is empty). Navigating from the root-node outwards through all the branches and sub-nodes returns the 4 colours "Marigold, Magenta, Magnolia and Mauve" (the 4 keys/entries) as a sorted sequence.
In general, if n is the number of keys/entries and n+ the number of nodes, the nodes are represented as a 256 bit ascii pointer vector ("IT-speak"!). In perhaps simpler-but-equivalent "math-speak", they are represented as a sparse 2-dimensional integer matrix of n+ rows (the nodes) and 256 columns (the ascii character-set). This forms a "DNA" sequence of characters/symbols that navigates from the root-node outwards and reconstructs each individual key/entry.
The second accompanying diagram demonstrates STrie's superiority over BTree in that having multiple branches per node results in less processing levels being required to locate a key/entry. The maximum of 256 branches for each node results in 8 times fewer levels (2 ^ 8 = 256), giving a rough-and-ready speed-limiter of n(log (n) / 8 in "big O" notation; 8 times faster.
Branches are represented as a 1-dimensional string-array of n+ rows. This forms a "junk-DNA" sequence of characters/symbols which do not affect the "node-navigation", but do contribute to the reconstruction of the key/entry. This "junk-DNA" usually comes at and/or near the end of keys (e.g. "ffalo" in "Buffalo"), but can occur anywhere (e.g. "est " in "West Carson" and "West Chester"). If a row-pointer is non-zero its column-position represents the ascii code concerned (e.g. a 123 in column 102 means "B"s are located in row 123, and a 4567 in column 165 means "u"s are located in row 4567).
The third accompanying striping/clustering diagram shows how the sparse integer matrix is refined by meta-data which indicates where non-zero row-pointers occur within the nodes (i.e. "where the action is"). The vertical stripes partition the ascii character-set into like-bands where data tends to cluster (e.g. alphabetics, numbers, etc.). The horizontal lines and points demarcate within each node where the data actually clusters which minimizes the number of linear-scans required. In this implementation if there are 3 or less row-pointers they are represented as point-vectors (e.g. "r", "g" and "u"), otherwise they are represented as a range-vector and a single point-vector (e.g. "B to Q" and "Z").
This approach is essential to maximize near key/entry location performance which is required to out-compete current algorithms that sort, retrieve and maintain data (e.g. QuickSort, BinarySearch and BTree etc.). These are required for applications such as symbolic-processors, sort-engines, spell-checkers and text-auto-fillers, dictionaries, relational and NoSQL databases, file-systems, etc.
The Downloads web-page contains working-examples and white-papers of STrie versus QuickSort (50+ percent faster), STrie versus BinarySearch (350% faster) and STrie versus BTree (100+ percent faster). The proof-of-concept code is written in MS VBA which was chosen for its ability to seamlessly integrate with Excel.
Although these are significant the compelling differentiator of the algorithm is its suitability for massive parallelization. Both data and processing can easily be spread across CPUs. The simplest way of doing this would be to front-end the algorithm with a triaging routine that distributes data (and hence processing) to 1 of 256 CPUs, based on the initial character of the STrie. A more sophisticated triaging routine would better-balance loads based on usage criteria.